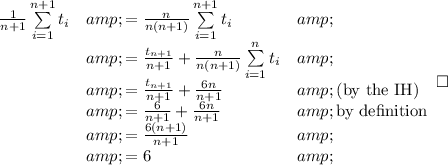Answer:
6
Explanation:
We can prove that every number after the second will be a six by induction.
Base case. Since
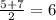 , so the third term is a six.
, so the third term is a six.
Inductive hypothesis. Fix the number of terms to be n and assume that
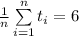
Inductive step. We will now show that
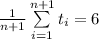 .
.
Notice that