Question

The total cost function for a product is C(x) = 750 ln(x + 10) + 1900

where x is the number of units produced.

(a) Find the total cost of producing 400 units. (Round your answer to the nearest cent.)

(b) Producing how many units will give total costs of $8500? (Round your answer to the nearest whole number.)

Answer 1

(a) $6,412.12

(b) 6624.

Explanation:

We have been given the total cost function for a product is
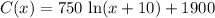`C(x)=750\text{ ln}(x+10)+1900`, where x is the number of units produced.

(a) To find the total cost of producing 400 units, we will substitute
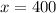`x=400` in our given formula.

`C(400)=750\text{ ln}(400+10)+1900`

`C(400)=750\text{ ln}(410)+1900`

`C(400)=750*6.0161571596983535+1900`

`C(400)=4512.117869773765125+1900`

`C(400)=6412.117869773765125`

`C(400)\approx 6412.12`

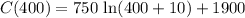
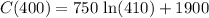
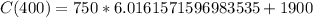
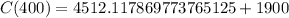
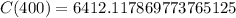
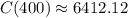
Therefore, the total cost of producing 400 units is $6,412.12.

(b) To find the number of units produced with total costs of $8500, we will substitute
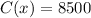`C(x)=8500` in our given formula.

`8500=750\text{ ln}(x+10)+1900`

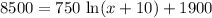
Switching sides:

`750\text{ ln}(x+10)+1900=8500`

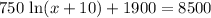
Subtract 1900 from both sides:

`750\text{ ln}(x+10)+1900-1900=8500-1900`

`750\text{ ln}(x+10)=6600`

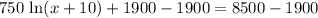
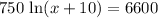
Now, we will divide both sides of our equation by 750.

`\frac{750\text{ ln}(x+10)}{750}=(6600)/(750)`

`\text{ ln}(x+10)=(44)/(5)`

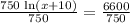
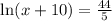
Using logarithm definition, we will get:

`x+10=e^{(44)/(5)}`

`x+10=6634.244006277887`

`x+10-10=6634.244006277887-10`

`x=6624.244006277887`

`x\approx 6624`

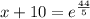
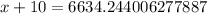
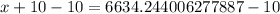
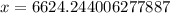
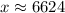
Therefore, producing 6624 units will give total costs of $8500.