Answer:
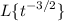 does not exists
does not exists
Explanation:
First lets introduce the definition of the Laplace transform (unitary version):
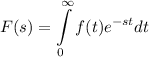 ;
;
Let's demonstrate why
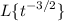 does not exists:
does not exists:
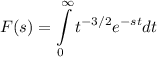
Writing st=u
⇒
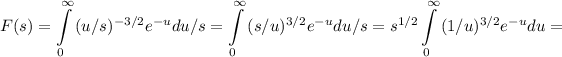
⇒
Where:
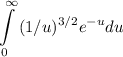
can be written as:
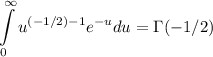
Where:
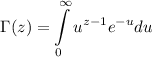
Is the Gamma Function
But:
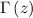 ; is only defined for z>0
; is only defined for z>0
Getting Demonstrated that
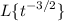 does not exists
does not exists