Question

I am trying to seperate 1/(s^2+1)(s^2+4) using partial fractions

I am used to doing the cover up method with fractions such as a/s+1 + b/s+2

however I am not sure how to do it with As+B/(s^2+1) ..etc and I hope that someone could help me with that

Answer 1

`(1/3)/(s^2+1)- (1/3)/(s^2+4)`

Explanation:

You already have the bottom in factors, write the partial fraction in the form As+b for each factor

`(1)/((s^2+1)(s^2+4)) =(As+B)/(s^2+1)+ (Cs+D)/(s^2+4)`

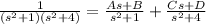
Multiply both sides by the bottom to stop using fractions:

`(1)/((s^2+1)(s^2+4))(s^2+1)(s^2+4)=((As+B)/(s^2+1)+ (Cs+D)/(s^2+4))(s^2+1)(s^2+4)`

`1=(As+B)(s^2+4)+(Cs+D)(s^2+1)}`

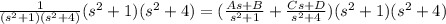
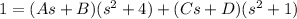
To find the value of the constants A, B, C, and D, separate the equation by the grade of the s, for example, all that multiplies s^3 in one equation like this:

`0=As^3+Cs^3`

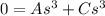
Because in the left part of the equation doesn't have constants multiplying the s^3 we put a zero in that side of the equation, do the same with s^2,s^1, and s^0

`0=4As+Cs\\0=Bs^2+Ds^2\\1=4B+D`

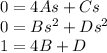
In this case, you can group the equation by constant to solve. First A and D, then B and C.

`As^3+Cs^3=0\\4As+Cs=0`

`Bs^2+Ds^2=0\\4B+D=1`

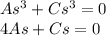
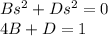
Solving for A and C:

`(A+C)(s^3)=0\\(4A+C)s=0`

`A+C=0\\4A+C=0\\\\`

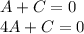
This system only has one solution A=0 and C=0.

Solving for B and D:

`(B+D)(s^2)=0\\4B+D=1`

`\\B+D=0\\4B+D=1\\\\D=-B\\4B-B=1\\3B=1\\B=1/3\\D=-1/3`

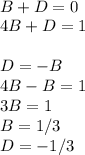
Then the solution is:

`(1/3)/(s^2+1)- (1/3)/(s^2+4)`