Answer:
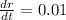 cm per second
cm per second
![(dS)/(dt)=320 square centimeter per second</strong></p><p><strong>Step-by-step explanation:</strong></p><p>We are given that volume of sphere </p><p>[tex]V=(4)/(3)\pi r^3](https://img.qammunity.org/2020/formulas/mathematics/college/jcjn0b7qm2l3zs2c1zaiv5p0q6j5fwejjz.png)
Volume of sphere is increasing at a constant rate
 cubic centimeters per second
cubic centimeters per second
We have to find the rate of radius at which increasing
when r= 10 cm
Differentiating w.r.t time
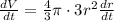
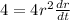
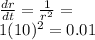 cm per second
cm per second
Now ,we are given that surface area of sphere
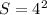
Differentiate w.r.t time then we get
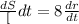
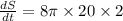
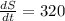 cm per second
cm per second