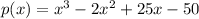Question

Find a polynomial function of lowest degree with real coefficients having zeroes of 2 and -Si (Show all work to earn credit.)

Answer 1

Answer: The required polynomial of lowest degree is
`p(x)=x^3-2x^2+25x-50`

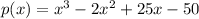
Step-by-step explanation: We are given to find a polynomial function of lowest degree with real coefficients having zeroes of 2 and -5i.

We know that

if x = a is a zero of a real polynomial function p(x), then (x - a) is a factor of the polynomial p(x).

So, according to the given information, (x - 2) and ( x + 5i) are the factors of the given polynomial.

Also, we know that complex zeroes occur in conjugate pairs, so 5i will also be a zero of the given polynomial.

This implies that (x - 5i) is also a factor of the given polynomial.

Therefore, the polynomial of lowest degree (three) with real coefficients having zeroes of 2 and -5i is given by

`p(x)=(x-2)(x+5i)(x-5i)\\\\\Rightarrow p(x)=(x-2)(x^2-25i^2)\\\\\Rightarrow p(x)=(x-2)(x^2+25)\\\\\Rightarrow p(x)=x^3-2x^2+25x-50`

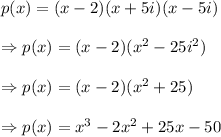
Thus, the required polynomial of lowest degree is
`p(x)=x^3-2x^2+25x-50`