Given:
The degree of polynomial = 9
Leading coefficient is negative.
To find:
The end behavior of the polynomial.
Solution:
Let the polynomial be P(x).
We have,
Degree of polynomial = 9, which is odd.
Leading coefficient is negative.
If the degree of a polynomial is odd and leading coefficient is negative, then
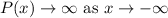
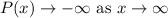
Therefore, the end behavior of the given polynomial is
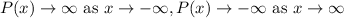 .
.