Question

A ball travels on a parabolic path in which the height (in feet) is given by the expression $-16t^2+64t+31$, where $t$ is the time after launch. What is the maximum height of the ball, in feet?

Answer 1

Maximum height, h(t) = 95 meters

Step-by-step explanation:

A ball travels on a parabolic path in which the height (in feet) is given by :

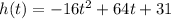`h(t)=-16t^2+64t+31`.............(1)

Where

t is the time after launch

We need to find the maximum height of the ball in feet. For maximum height,

`(dh(t))/(dt)=0`

`(d(-16t^2+64t+31))/(dt)=0`

`-32t+64=0`

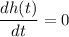
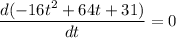
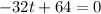
t = 2

Put the value of t in equation (1) as :

`h(t)=-16(2)^2+64(2)+31`

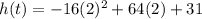
h(t) = 95 meters

So, the maximum height of the ball is 95 meters. Hence, this is the required solution.