Question

Find out if the 3 positions are on the same line or not (3,2,0) (1, -1,2) (5,5, 2)

Answer 1

The three positions are not on the same line.

Explanation:

We have three points: A:(3,2,0), B:(1,-1,2) and C:(5,5,2).

Let's build a vector that goes from one point to another; that vector will be the director of a line (if we draw a vector that goes from A to B, that vector will be the direction of the line that pass by A and B because it does not change). In order to build that vector, let's subtract B from A:

`A-B=(3,2,0)-(1,-1,2)=(2,3,-2)`

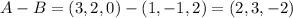
The equation of a line is:

`p=p_0+rt`

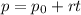
Where p is every singular point of the line,
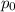`p_0` is a particular point of the line (any that we are sure that it is on the line), r is the director vector and t is the independent variable.

Now we have the director vector: (2,3,-2), and we can verify that A and B are on the line:

`p=p_0+(2,3,-2)t`

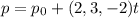
Because there is a value for t that satisfies both A and B: If we do
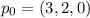`p_0=(3,2,0)` and t=0, we are going to obtain the point p=A; and if we do t=-1, we are going to obtain p=B. Let's see that:

`p=(3,2,0)+(2,3,-2)*0=(3,2,0)\\p=A\\p=(3,2,0)+(2,3,-2)*-1=(1,-1,2)\\p=B\\`

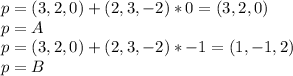
If C is also in the same line, C must accomplish the equation:
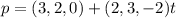`p=(3,2,0)+(2,3,-2)t`, so:

`C=(5,5,2)=(3,2,0)+(2,3,-2)t`

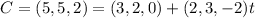
Let's simplify the equation writing the parametric equation, which is just to write the equation for each dimension:

`5=3+2t\\5=2-3t\\2=-2t\\`

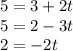
You can verify that there is not a value of t that satisfies all three equations, so, the point C is not on the same line as A and B; which means that A, B and C are not on the same line.