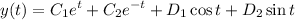Question

Find the general solution to:

y^(4) - y =0

Answer 1

`$y(t) = C_1 e^(t) + C_2 e^(-t) + D_1 \cos t + D_2 \sin t }$`

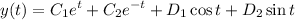
Explanation:

The equation is a linear differential equation: y⁽⁴⁾- y = 0

We assume the form of the solution y(t) is
`$y(t)=C_(1) e^{\alpha_(1) t} + C_(2) e^{\alpha_(2) t} + C_(3) e^{\alpha_(3) t} + C_(4) e^{\alpha_(4) t} $`

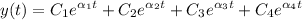
where
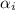`$\alpha_(i)` are the roots of the auxiliary equation.

So, use the auxiliary equation:
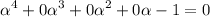`$\alpha^4 + 0 \alpha^3 + 0 \alpha^2 + 0 \alpha -1 =0$` to find the roots; the values are : α₁ = 1, α₂ = -1, α₃ = i, α₄ = -i

Then inserting
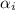`$\alpha_(i)` values in the assumed solution

⇒
`$y(t)=C_1 e^(t) + C_2 e^(-t) + C_(3) e^(it) + C_(4) e^(-it) $`

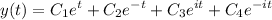
Also, because the last 2 terms have complex power, the solution can be written with cosine and sine terms:

Using the Euler's formula:
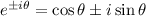`e^( \pm i\theta ) = \cos \theta \pm i\sin \theta`, we can rewrite the solution as:

`$y(t) = C_(1) e^(t) + C_(2) e^(-t) + C_(3) e^(i t) + C_(4) e^(-i t)` =
`C_(1) e^(t) + C_(2) e^(-t) + C_(3) ( \cos t + i \sin t ) + C_(4) ( \cos t - i \sin t ) = C_(1) e^(t) + C_(2) e^(-t) + \cos t ( C_(3) + C_(4) ) + \sin t (i C_(3) - i C_(4) ) = C_(1) e^(t) + C_(2) e^(-t) + D_(1) \cos t +D_(2) \sin t$`

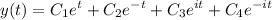Where:
`$D_1 = C_3 + C_4$ and $D_2= i ( C_3 - C_4 )$`

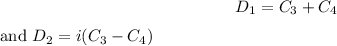
Finally the solution for de linear differential equation y^(4) - y =0 is:

`$y(t) = C_1 e^(t) + C_2 e^(-t) + D_1 \cos t + D_2 \sin t }$`