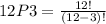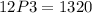Question

From 12 prepared songs, a band

chooses 3 to perform on a TV show. One
song will be played at the beginning of
the show, one in the middle, and one at
the end. Tell how many different set lists
are possible. Then tell if the situation
involves permutations or combinations.

Answer 1

1320 different set lists are possible

Explanation:

We have a set of 12 elements (12 songs)

There can be NO songs repeatedly

The order of the songs is important because One song will be played at the beginning of the show, one in the middle, and one at the end.

So as the order of selection is important we must use permutations.

The formula for permutations is:

`nPr=(n!)/((n-r)!)`

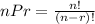
where n is the number of items you can choose and choose r from them

In this case we know that:

`n=12`,
`r=3`

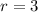
Then:

`12P3=(12!)/((12-3)!)`

`12P3=(12!)/(9!)`

`12P3=1320`