Let
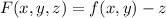 . The tangent plane to
. The tangent plane to
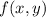 at (1, 2, -6) has equation
at (1, 2, -6) has equation

We have
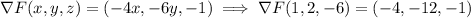
Then the tangent plane has equation
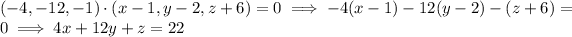
Let
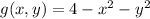 , and
, and
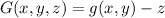 . The tangent plane to
. The tangent plane to
 at a point
at a point
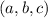 is
is
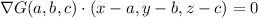
We have
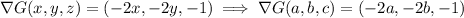
so that this plane has equation
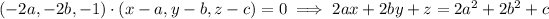
In order for this plane to be parallel to the previous plane, we need to have
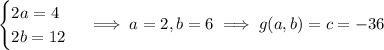
so the point we're looking for is (2, 6, -36).