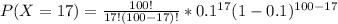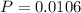Answer: Option B
Explanation:
We can use the binomial formula to solve this problem.
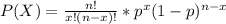
Where p is the probability of success, n is the sample size and x is the number of successes expected.
Note that in this case
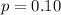 (probability of an adult passing the fitness test)
(probability of an adult passing the fitness test)

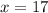
Then we calculate the probability