Question

Dx + (x cot y+ sin y)dy=0 ,solve the DE

Answer 1

`\mathrm dx+(x\cot y+\sin y)\,\mathrm dy=0`

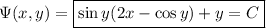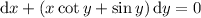
Multiply both sides by
`\sin y`:

`\sin y\,\mathrm dx+(x\cos y+\sin^2y)\,\mathrm dy=0`

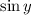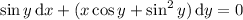
The ODE is now exact, since

`(\partial(\sin y))/(\partial y)=\cos y`

`(\partial(x\cos y+\sin^2y))/(\partial x)=\cos y`

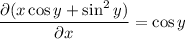
so there exists a solution of the form
`\Psi(x,y)=C`. This solution satisfies

`(\partial\Psi)/(\partial x)=\sin y`

`(\partial\Psi)/(\partial y)=x\cos y+\sin^2y`

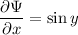
Integrating both sides of the first PDE wrt
`x` gives

`\Psi(x,y)=x\sin y+f(y)`

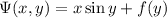
and differentiating wrt
`y` gives

`(\partial\Psi)/(\partial y)=x\cos y+\sin^2y=x\cos y+(\mathrm df)/(\mathrm dy)`

`\implies(\mathrm df)/(\mathrm dy)=\sin^2y=\frac{1-\cos2y}2`

`\implies f(y)=\frac y2-\frac{\sin2y}4+C`

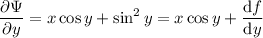
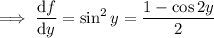
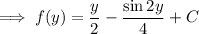
So the ODE has solution

`\Psi(x,y)=x\sin y+\frac y2-\frac{\sin2y}4=C`

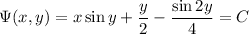
which can be rewritten and simplified as

`\Psi(x,y)=\boxed{\sin y(2x-\cos y)+y=C}`