Question

Show the following are or are not a basis for the given vector space. Explain why or why not it is a basis. (a) (1,2,3), (4,5,6), (2,3,1) in R3 (b) (1,2,3), (4,5,6), (7,8,9) in R3 (c) V1, V2, V3, V4 in R3 (d) (1,0,1),(0,1,2) in W = {(a, b, a +26) a, b E R}

Answer 1

a)We need to check that all vectors from R^3 can be written as linear combination of the given vectors. This is

`\alpha(1,2,3)+\beta(4,5,6)+\gamma(2,3,1)=(x,y,z)`

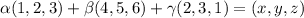
where
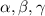`\alpha,\beta,\gamma` are real numbers and
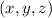`(x,y,z)` is a generic vector from R^3. This statement is equivalent to the fact that the system of linear equations with associated matrix

`A=\left[\begin{array}{ccc}1&4&2\\2&5&3\\3&6&1\end{array}\right]`

has solution for every independent term
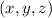`(x,y,z)`. This can be easily check calculating the determinant of the matrix A. Then, according to Sarrus' rule:

`\det A = (5+36+24)-(30+8+18)=65-56=9.`

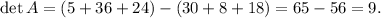
Therefore, the system of vectors is a basis for R^3.

b) In this case we follow the same reasoning. The matrix associated to the system of linear equations is

`B=\left[\begin{array}{ccc}1&4&7\\2&5&8\\3&6&9\end{array}\right],`

and its determinant is

`\det B=(45+96+84)-(105+72+48)=225-225=0.`

The fact that the determinant is zero implies that the system is not solvable for some independent vectors, which is equivalent to that not all vector of R^3 can be written as linear combination of the given system of vectors. Then, this system is not a basis of R^3.

c) This system cannot be a basis of R^3 because it has four vectors. Notice that the dimension of this space is 3, so every basis has exactly 3 vectors, no less, no more.

d) Clearly the two vectors are linearly independent, because the first one is not proportional to the second one. Then, we only need to check if every vector of W can be written as a linear combination of (1,0,1) and (0,1,2).

In particularly, take a=b=1, which gives the vector (1,1,27) in W. Now, notice that for the first to components compels the linear combination

`1\cdot (1,0,1)+1\cdot(0,1,2) = (1,1,3).`

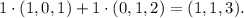
Then, there is, at least a vector of W that cannot be written as linear combination of the given vector. Therefore, (1,0,1) and (0,1,2) is not a basis for W.

Explanation:

a) and b) This to exercises are very similar. The core of the reasoning is that the problem of determine if a system of vector is linearly independent is equivalent to solve a system of linear equations. So, if we form a matrix with columns the vectors of the system we can deduce the following statements:

1. If the determinant is different from zero the vectors are linearly independent.
2. If the determinant is zero the vectors are linearly dependent.

Remember that a basis must be linearly independent.

c) Here we must recall that in every space, the number of linearly independent vectors are, at must, the dimension of the space. That is why in R^3 every system of linearly independent vectors has, at most, three vector; in R^4 four and so on.

d) This is a little tricky. We have that the vectors are linearly independent, but as we are dealing with a subspace of R^3 instead of the whole space we must be more carefully. Then we need to check that every element of W can be written as linear combination of the given vectors.