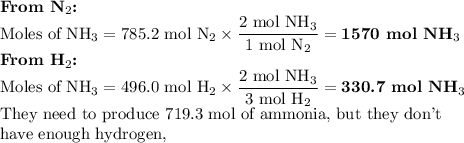Question

A chemical company makes ammonia by reacting with nitrogen and hydrogen and company needs to make 70 badges of ammonia for a client each batch contains 175 g they have 22,000 g of nitrogen and 1000 g of hydrogen will I be able to make enough ammonia to fill the order

Answer 1

`\boxed{\text{No}}`

Step-by-step explanation:

This is a disguised limiting reactant problem.

We are given the masses of two reactants and asked to determine if we have enough to make a given amount of product.

1. Calculate the mass of NH₃ needed.

`\text{Mass of NH}_(3) = \text{70 batches} * \frac{\text{175 g}}{\text{1 batch}} = \text{12 250 g}`

2. Assemble the information

We will need a balanced equation with masses and molar masses, so let’s gather all the information in one place.

M_r: 28.02 2.016 17.03

N₂ + 3H₂ ⟶ 2NH₃

Mass/g: 22 000 1000 12 250

3. Calculate the moles of NH₃ needed

`\text{Moles of NH$_(3)$} = \text{12 250 g} * \frac{\text{1 mol}}{\text{17.03 g}} = \text{719.3 mol}`

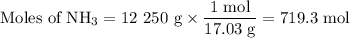
4. Calculate the moles of each reactant

`\text{Moles of N$_(2)$} = \text{22 000 g} * \frac{\text{1 mol N$_(2)$}}{\text{28.02 g N$_(2)$}} = \text{785.2 mol NH$_(3)$}\\\text{Moles of H$_(2)$} = \text{1000 g} * \frac{\text{1 mol H$_(2)$}}{\text{2.016 g H$_(2)$}} = \text{496.0 mol H$_(2)$}`

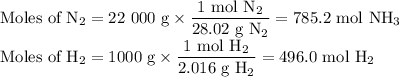
5. Calculate the moles of NH₃ from each reactant

`\textbf{From N$_(2)$:}\\\text{Moles of NH$_(3)$} = \text{785.2 mol N$_(2)$} * \frac{\text{2 mol NH$_(3)$}}{\text{1 mol N$_(2)$}} = \textbf{1570 mol NH$_(3)$}\\\textbf{From H$_(2)$:}\\\text{Moles of NH$_(3)$} = \text{496.0 mol H$_(2)$} * \frac{\text{2 mol NH$_(3)$}}{\text{3 mol H$_(2)$}} = \textbf{330.7 mol NH$_(3)$}\\\text{They need to produce 719.3 mol of ammonia, but they don't}\\\text{have enough hydrogen,}`
`\boxed{\textbf{No,}}\\\text{They will not be able to make enough ammonia to fill the order.}`