For this case we have that by definition, a linear equation is of the form:

Thus, we have the following options:
Option A:
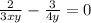
It is not a linear equation !!
Option B:
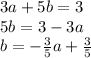
It is a linear equation!
Option C:
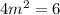
It is a quadratic equation, the exponent of the variable is 2.
Option D:

It is a quadratic equation, the exponents are quadratic!
Answer:
Option B