Question

The graph of g(x) = 5x is a transformation of the graph of f(x) = x. Which of the following describes the transformation?

a)

reflected across the x-axis


b)

reflected across the y-axis


c)

compressed vertically


d)

stretched vertically

Answer 1

The term which describes the transformation is:

Option: d

d) stretched vertically

Explanation:

We have a parent function i.e. the original function f(x) as:

`f(x)=x`

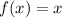
We know that the transformation of the type:

f(x) to a f(x) either vertically stretch or vertically squeeze the function depending on a.

If a>1 then the transformation is a vertical stretch.

and if a<1 then the transformation is a vertical squeeze.

Here a=5>1

Hence, the function g(x) i.e.

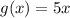`g(x)=5x` is a vertical stretch of the function f(x).

Answer 2

The graph is stretched vertically.

Option D is correct.

Explanation:

The parent function is f(x) = x

The other function is g(x) = 5x

The value of a describes the vertical stretch of the graph

if a>1 then the graph is vertically stretched

Here g(x) = 5x

a = 5

as a>1, so, the graph is stretched vertically.

Option D is correct.