Question

Solve the inequality and express in interval notation and graph its solution on a number line

6. x^2 > 9x – 18

Answer 1

x ∈ (-∞, 3) U (6, ∞).

Explanation:

`x^2> 9x - 18`

`x^2 - 9x + 18> 0`

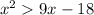
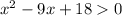
We use factorization and optain

`(x-6)(x-3)> 0`

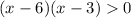
Then, we have two critical points: x=3 and x=6. Now:

(i) for x < 3 we have that x-6 <0 and x-3 <0. Then (x-6)(x-3) > 0.

(ii) for 3 < x < 6 we have that x -6 <0 and x -3 > 0. Then (x-6)(x-3) < 0.

(iii) for x > 6 we have that x-6 >0 and x-3 > 0. Then, (x-6)(x-3) > 0.

conditions (i) and (iii) satisfy the inequatliy, then the solution is x ∈ (-∞, 3) U (6, ∞).

The graph is in the picture below.