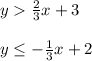Which graph shows the solution to the system of linear inequalities? y > 2/3x + 3 y ≤ 1/3x + 2 option B is the answer (pictured)

Question

asked May 7, 2020 230k views

2 Answers

Suleman Khan · Answer 1 · 2020-05-13T01:05:50+0000

Answer:

Observe the attached image.

Explanation:

We have the following linear inequalities

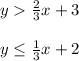
$y > (2)/(3)x + 3\\\\y \leq (1)/(3)x + 2$

Graph the lines corresponding to each inequality

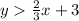y > (2)/(3)x + 3 →
y = (2)/(3)x + 3

Cut with the y axis:

y = 3

Cut with the x axis:

0 = (2)/(3)x + 3

-3 = (2)/(3)x

x = -4.5

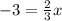
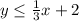$y \leq (1)/(3)x + 2$ →
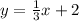
y = (1)/(3)x +2

Cut with the y axis:

y = 2

Cut with the x axis:

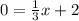
0 = (1)/(3)x + 2

-2 = (1)/(3)x

x = -6

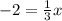
Now graph the two lines

For
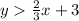
y > (2)/(3)x + 3

The region is made up of all the points that are above the line
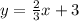
y =(2)/(3)x + 3

For
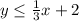
$y \leq (1)/(3)x + 2$

The region is made up of all the points that are on the line and below
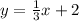
y = (1)/(3)x +2

The final region will be the interception of both regions

Observe the attached image.

The system shown in the image you attached is:

$y > (2)/(3)x + 3\\\\y \leq -(1)/(3)x + 2$