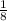Question

A cone shaped paper water cup has a height of 12 cm and a radius of 6 cm. If the cup is filled with water to half its height, what portion of the volume of the cup is filled with water?

Exactly ___ of the cup is filled with water.
(Type a simplified fraction)

Answer 1

Exactly _
`(1)/(8)`__ of the cup is filled with water.

Explanation:

The formula to calculate the volume of a cone is:

`V=(1)/(3)\pi r^2h`

Where

r is de radius

h is the height

So the volume of the cone is:

`V=(1)/(3)\pi (6)^2*12`

`V=144\pi\ cm^3`

The angle z that is opposite the radius of the cone is:

`tan(z)=(r)/(h)=(6)/(12)\\\\z =tan^(-1)((6)/(12))\\\\z=26.565\°`

The amount of water that fills half the cone occupies the volume of a cone with radius R, height
`(h)/(2)` and angle z = 26.565°

Therefore we have that:

`(h)/(2)=6\ cm`

and

`tan(z)=(r)/(h)=(R)/(6)`

`(r)/(h)=(R)/(6)`

`(6)/(12)=(R)/(6)`

`(R)/(6)=0.5`

`R=3`

Then portion of the volume of the cup is filled with water is:

`V=(1)/(3)\pi (3)^2(6)`

`V=18\pi\ cm^3`

`v =(18\pi\ cm^3)/(144\pi\ cm^3)\\\\\V =(1)/(8)`

Answer 2

The portion of the volume of the cup that is filled with water is
`(1)/(8)`

Explanation:

step 1

Find the volume of the paper water cup

The volume of the cone is equal to

`V=(1)/(3)\pi r^(2)h`

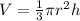
we have

`r=6\ cm`

`h=12\ cm`

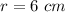
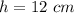
substitute

`V=(1)/(3)\pi (6)^(2)(12)`

`V=144\pi\ cm^(3)`

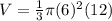
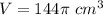
step 2

If the cup is filled with water to half its height, find out what portion of the volume of the cup is filled with water

Remember that

If two figures are similar, then the ratio of its volumes is equal to the scale factor elevated to the cube

In this problem the similar cone has half the height of the complete cone

so

The scale factor is equal to 1/2

therefore

The volume of the cup that is filled with water is equal to the volume of the complete cup by the scale factor elevated to the cube

`V=(1/2)^(3)(144\pi)=(1/8)144\pi\ cm^(3)`

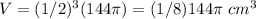
therefore

The portion of the volume of the cup that is filled with water is

`(1)/(8)`