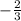Question

What is the slope of the line with the following equation?


`2x+3y=2`

Answer 1

slope = -
`(2)/(3)`

Explanation:

The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

Rearrange 2x + 3y = 2 into this form

Subtract 2x from both sides

3y = - 2x + 2 ( divide all terms by 3 )

y = -
`(2)/(3)` x +
`(2)/(3)` ← in slope- intercept form

with slope m = -
`(2)/(3)`

Answer 2

QUESTION

Your equation is 2x+3y=2 and you need to find the slope.

EXPLANATION

There are many ways to find the slope with an equation like this. I'm going to change the equation into slope-intercept form.

Slope-intercept form is formatted like this:

y=mx+b

m represents the slope. The first thing you need to do is leave 3y alone to change the equation into slope-intercept form. That means you need to subtract 2x from both sides.

`2x+3y=2 \rightarrow 3y=2-2x\ or\ 3y=-2x-2`

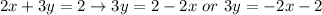
The next thing you need to do is leave y alone, just like the slope-intercept form example. To leave y alone, you need to divide 3y by 3.

`(3y)/(3)=(-2x-2)/(3) \\ \\ y=-(2)/(3)x-(2)/(3)`

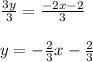
Now the equation has been changed to slope-intercept form. In the equation, m has been replaced by
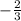`-(2)/(3)`, which means that is your answer.

Answer:
`-(2)/(3)`