Question

The figure below shows triangle NRM with r2 = m2 + n2:

Triangle NRM has legs m and n, and r is the length of its longest side.

Ben constructed a right triangle EFD with legs m and n, as shown below:

Triangle EFD has legs m and n and hypotenuse f.

He made the following table to prove that triangle NRM is a right triangle:


Statement Reason
1. r2 = m2 + n2 Given
2. f2 = m2 + n2 Pythagorean Theorem
3. f2 = r2 Substitution
4. f = r ?
5. Triangle NRM is congruent to triangle EFD SSS Postulate
6. Angle NRM is a right angle CPCTC
7. Triangle NRM is a right triangle Angle NRM is a right angle

Which reason best fits statement 4?
SAS postulate
AAS postulate
Square Root Property of Equality
Triangle Proportionality Theorem

Answer 1

Answer: Square Root Property of Equality

Explanation:

If we have an equation with a perfect square on both sides , then Square Root Property of Equality says that we can take square root on both the sides to solve the equation and the equality remains same.

From the given proof , the statement 3. gives
`f^2=r^2`

Then by applying Square Root Property of Equality, we can take square root on both sides, we get

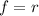`f=r` which is the statement 4.

Hence, the correct answer is "Square Root Property of Equality".

Answer 2

The correct answer is square root property of equality.

Explanation:

Triangle NRM has legs m and n and r is the length of its longest side.

Ben constructed a right triangle EFD with legs m and n and hypotenuse f.

It means that both the triangles have legs with sides m and n beside that the third side of NRM is equal to the third side EFD, i.e ⇒ f =r(statement 4) which is proved by the square root property of equality.

Thus the correct option is square root property of equality....