Answer:
Problem 1:
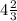
Problem 2: 2.5
Problem 3: 0
Explanation:
If it tells you it is arithmetic, it is give you a huge hint. Arithmetic sequences have common differences. That means if you do:
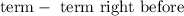 you will get the same number.
you will get the same number.
Problem 1:
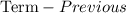

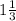
So the common difference is
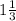 .
.
The next term can be found by adding
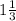 to the previous.
to the previous.
 .
.
Problem 2:
0.5 , 0.7 , ....
Start with finding the common difference:

 is the common difference.
is the common difference.
The common difference can be used to find the next term given it's previous term.
So you have:
First term is 0.5 .
Second term is 0.7 .
Third term is 0.7+ 0.2=0.9 .
Fourth term is 0.9 + 0.2=1.1 .
You could find a pattern so you don't have to find all the terms before the 11th.
So let's start over:
First term is 0.5 .
Second term is 0.5+0.2 .
Third term is 0.5+0.2(2).
Fourth term is 0.5+0.2(3).
.............
nth term is 0.5+0.2(n-1).
The thing in parenthesis was always one less than term number we wanted to find.
The 11th term is given by 0.5+0.2(10).
Let's simplify:
0.5+0.2(10)
0.5+2
2.5
2.5 is the 11th term.
Problem 3:
We are going to do something similar that we did for the problem before this one.
First common difference is given by:
Term-Previous
24-27
-3
The common difference is -3. (It is going down by 3 each time.)
The tenth will be given by 27+-3(9).
Let's simplify:
27+-3(9)
27+-27
0