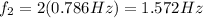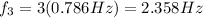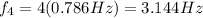Question

Find the fundamental frequency and the next three frequencies that could cause standing-wave patterns on a string that is 30.0 m long, has a mass per length of 9.00 - 10#3 kg/m, and is stretched to a tension of 20.0 N.

Answer 1

0.786 Hz, 1.572 Hz, 2.358 Hz, 3.144 Hz

Step-by-step explanation:

The fundamental frequency of a standing wave on a string is given by

`f=(1)/(2L)\sqrt{(T)/(\mu)}`

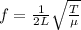
where

L is the length of the string

T is the tension in the string

`\mu` is the mass per unit length

For the string in the problem,

L = 30.0 m

`\mu=9.00\cdot 10^(-3) kg/m`

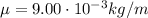
T = 20.0 N

Substituting into the equation, we find the fundamental frequency:

`f=(1)/(2(30.0))\sqrt{(20.0)/((9.00\cdot 10^(-3))}=0.786 Hz`

The next frequencies (harmonics) are given by

`f_n = nf`

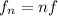
with n being an integer number and f being the fundamental frequency.

So we get:

`f_2 = 2 (0.786 Hz)=1.572 Hz`

`f_3 = 3 (0.786 Hz)=2.358 Hz`

`f_4 = 4 (0.786 Hz)=3.144 Hz`