Answer:
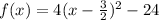
The minimum occurs at
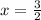 .
.
Explanation:
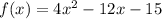
The
 in
in
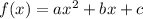 is the same
is the same
 in
in
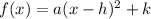 where:
where:
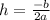 and
and
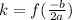 .
.
So let's find
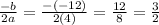 .
.
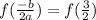 .
.
To find
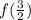 , we must use the expression that
, we must use the expression that
 is and evaluate it for
is and evaluate it for
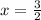 , like so:
, like so:
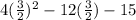
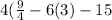
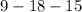

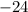
So the vertex form is
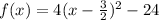 .
.
-----------------Another way----------------------------
You could just complete the square.
I like to use the following to help me formulate the process:
 .
.
Let's start. My formula requires coefficient of
 to be 1 so factor out the 4 from the first two terms:
to be 1 so factor out the 4 from the first two terms:
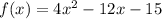
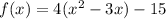
Now we are going to add the
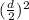 to complete the square; whatever you add in you must also subtract out.
to complete the square; whatever you add in you must also subtract out.
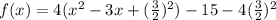
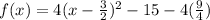

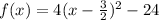
-----------------So anyways either way you choose....-----------------------
The minimum or maximum will occur at the vertex. Since
 is positive the parabola is open up and therefore does have a minimum.
is positive the parabola is open up and therefore does have a minimum.
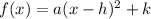 tells us the vertex is
tells us the vertex is
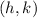 .
.
So h is the x-coordinate of the vertex.
So the minimum occurs at
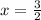 .
.