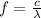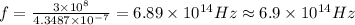Answer:
(c) 6.91x10^14 Hz
Step-by-step explanation:
Find the level energy of n=2 and n=5, using the formula:
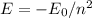
where
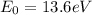
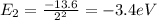
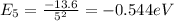
To jump from n=2 to n=5 the electron absorbs a photon with energy equal to
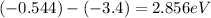 , using the next formula to find specific wavelength
, using the next formula to find specific wavelength
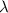 to that energy
to that energy
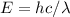
Where
 is the speed of light (
is the speed of light (
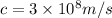 ) and
) and
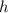 is Planck's constant (
is Planck's constant (
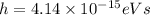 ). Solve for
). Solve for
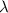 :
:
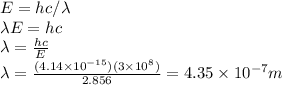
The frequency of this wavelength is calculated with this formula: