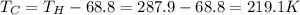Question

A Carnot engine has an efficiency of 23.9%. It operates between constant-temperature reservoirs differing in temperature by 68.8°C. In kelvins, what are (a) the temperature of the hot reservoir and (b) the temperature of the cold reservoir?

Answer 1

(a) 287.9 K

The efficiency of the engine is given by

`\eta = 1-(T_C)/(T_H)`

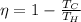
where

Tc is the temperature of the cold reservoir

Th is the temperature of the hot reservoir

We can rewrite the two temperatures as

`T_c = T_h - 68.8 K`

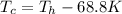
(because differences in Kelvin are equal to differences in Celsius)

So we can rewrite the 1st equation as

`\eta = 1-(T_H - 68.8)/(T_H) =1-1+(68.8)/(T_H)=(68.8)/(T_H)`

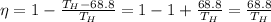
We also know the efficiency:

`\eta = 23.9\% = 0.239`

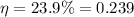
So we can re-arrange the previous equation to find the temperature of the hot reservoir:

`T_H = (68.8)/(0.239)=287.9 K`

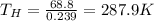
(b) 219.1 K

The temperature of the cold reservoir can be found as:

`T_C = T_H - 68.8 = 287.9 - 68.8=219.1 K`