Question

A fluid of density 900 kg/m3 passes through a converging section of an upstream diameter of 50 mm and a downstream diameter of 25 mm. Pressure difference across the area reduction is - 40 kN/m2 Determine the downstream velocity and the volume flow rate if the flow is ideal. i. Determine the downstream velocity if the flow is not ideal and has a velocity coefficient of Cy = 0.89.

Answer 1

Q= 4.6 × 10⁻³ m³/s

actual velocity will be equal to 8.39 m/s

Step-by-step explanation:

density of fluid = 900 kg/m³

d₁ = 0.025 m

d₂ = 0.05 m

Δ P = -40 k N/m²

C v = 0.89

using energy equation

`(P_1)/(\gamma)+(v_1^2)/(2g) = (P_2)/(\gamma)+(v_2^2)/(2g)\\(P_1-P_2)/(\gamma)=(v_2^2-v_1^2)/(2g)\\(-40* 10^3* 2)/(900)=v_2^2-v_1^2`

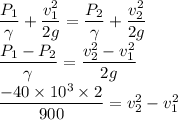
under ideal condition v₁² = 0

v₂² = 88.88

v₂ = 9.43 m/s

hence discharge at downstream will be

Q = Av

Q =
`(\pi)/(4)d_1^2 * v`

Q =
`(\pi)/(4)0.025^2 * 9.43`

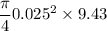
Q= 4.6 × 10⁻³ m³/s

we know that

`C_v =(actual\ velocity)/(theoretical\ velocity )\\0.89 =(actual\ velocity)/(9.43)\\actual\ velocity = 8.39m/s`

hence , actual velocity will be equal to 8.39 m/s