Answer: 350
Explanation:
Given : A survey of a random sample of students found that 14 preferred
country music, 16 preferred rock, 5 preferred classical, and 10
preferred pop.
Sample size :
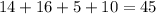
Number of students prefer country or rock music= 14+16=30
Now, the proportion of students prefer country or rock music =
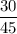

Total students in the school= 630
Predicted number of students in the school prefer country or rock music=
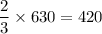
The proportion of students prefer classical music =
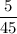

Predicted number of students in the school prefer classical music=

Now, the predicted number of students in the school prefer more country or rock music than prefer classical music = 420-70=350