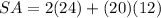Answer:
The total surface area of the prism is

Explanation:
we know that
The two diagonals of a rhombus are perpendicular and bisect each other
All sides are congruent
The surface area of a prism is equal to
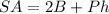
where
B is the area of the base of prism
P is the perimeter of the base of prism
h is the height of the prism
step 1
Find the length side of the rhombus
Applying Pythagoras Theorem
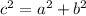
we have
c is the length side of the rhombus
a and b are the semi diagonals of the rhombus
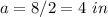
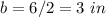
substitute
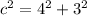
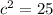
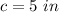
step 2
Find the perimeter of the base P
The perimeter of the rhombus is equal to
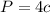

step 3
Find the area of the base B
The area of the rhombus is
![B=(1)/(2)[D1*D2]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/u5qtc7dkd3etcssd45yd52b44wqs6wfo02.png)
D1 and D2 are the diagonals of the rhombus
substitute
![B=(1)/(2)[8*6]=24\ in^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/5633gopgevep9yawlnbgesa6mkkt85x2gu.png)
step 3
Find the surface area of the prism
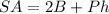
substitute the values