Answer:
D.Its lateral surface area is equal to the product of its perpendicular height and the circumference of its base.
Explanation:
Right circular cylinder :It consist of cylinder and two circular bases .
Let a right circular cylinder of radius r and height h.
Lateral surface area of right circular cylinder =

Where r=Radius of cylinder
h=Height of cylinder
Total surface area of cylinder=
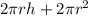
Volume of right circular cylinder =
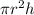
Circumference of circular base =
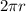
Hence, the lateral surface area of right circular cylinder =
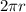
Therefore, option D is true.
D.Its lateral surface area is equal to the product of its perpendicular height and the circumference of its base.