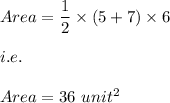Question

The four points (−2, 5), (−2, −1), (5, −1), and (3, 5) are the vertices of a polygon. What is the area, in square units, of this polygon?

27 units2
33 units2
36 units2
51 units2

Answer 1

the area, in square units, of this polygon is 36 units2

Answer 2

The area of the given Polygon is:

`36\ unit^2`

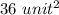
Explanation:

The polygon is in the shape of the trapezoid with two bases AB and CD and altitude as: AD

Now we know that the area of trapezoid is given by:

`\text{Area}=(1)/(2)* (\text{Sum of bases})* \text{Altitude}`

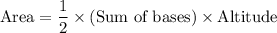
i.e.

Here

`\text{Area}=(1)/(2)* (AB+CD)* AD`

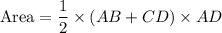
Now, we find the length of AB,CD and AD using distance formula.

A is located at (-2,5)

B at (3,5)

C at (5,-1)

D at (-2,-1)

`AB=√((-2-3)^2+(5-5)^2)\\\\i.e.\\\\AB=√((-5)^2+0^2)\\\\i.e.\\\\AB=√(25)\\\\i.e.\\\\AB=5\ units`

`CD=√((5-(-2))^2+((-1)-(-1))^2)\\\\i.e.\\\\CD=√(7^2+0^2)\\\\i.e.\\\\CD=7\ units`

`AD=√((-2-(-2))^2+(5-(-1))^2)\\\\i.e.\\\\AD=√(0^2+6^2)\\\\i.e.\\\\AD=6\ units`

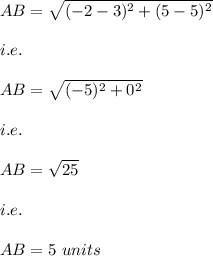
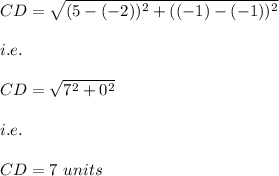
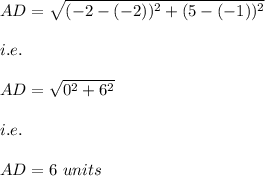
Hence, the area of Trapezoid is:

`Area=(1)/(2)* (5+7)* 6\\\\i.e.\\\\Area=36\ unit^2`