Answer:
Explanation:
I used Pascal's Triangle to the 19th row (that took forever!!) and the leading coefficients are as follows:
1, 18, 153, 816, 3060, 8568, 18564, 31824, 43758, 48620, 43758, 31824, 18564, 8568, 3060, 816, 153, 18, 1
You need the middle term so we can stop the expansion at 48,620. We will choose an a and a b from the binomial to be a = x and b = 1/x. Start with the coefficients from above in order and follow the pattern:
1(x)¹⁸(1/x)⁰ + 18(x)¹⁷(1/x)¹ + 153(x)¹⁶(1/x)² + 816(x)¹⁵(1/x)³ + 3060(x)¹⁴(1/x)⁴ + 8568(x)¹³(1/x)⁵ + 18564(x)¹²(1/x)⁶ + 31824(x)¹¹(1/x)⁷ + 43758(x)¹⁰(1/x)⁸ + 48620(x)⁹(1/x)⁹
That last term there is the middle term. Simplified it looks like this:
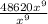which is simplified to just 48620