Answer:
D
Explanation:
Terms are separated by addition and subtraction symbols.
Polynomials consist of terms that are constant and/or variable. The variable terms must have 0 or positive exponents. Polynomials will not consist of division of variable expressions.
Examples of polynomials:


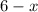
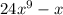
Examples of non-polynomials:
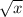
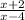
In general a polynomial when written in standard form should be comparable to:
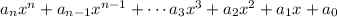
where the
 's could be zero and all the exponents,n, are positive or 0.
's could be zero and all the exponents,n, are positive or 0.
D is comparable since all of these are 0 except
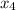 which is 1 and
which is 1 and
 which is -2.
which is -2.
Also the other choices have either division by variable expressions and/or negative exponents on variables.