Answer:
135.86≈ 136
Explanation:
As Given in figure 1:
In ΔABC, m∠A = 72°, m∠B = 16° and c = 61 , where a, b, and c are lengths of side of ΔABC.
To find: Perimeter of triangle = ?
Sol: In ΔABC,
m∠A + m∠B + m∠C = 180° (sum of angles of a triangle)
m∠C = 180° - (72° + 16°)
m∠C = 92°
Now Using Sine Rule:
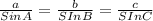
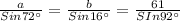
Now,
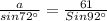
∴
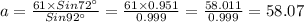
In the same way,
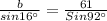
∴
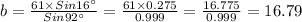
Therefore, a = 58.07 ≈ 58, b = 16.79 ≈ 17 and c = 61
Now, Perimeter of ΔABC = a + b + c = 58 + 17 + 61 = 136