Question

Find two linearly independent power series solutions about the point x0 = 0 of

(x^2 ? 4)y"+ 3xy' + y = 0. State the minimum radius of convergence, and explain
why it is the minimum of radius of convergence.

Answer 1

Assume a solution of the form

`y=\displaystyle\sum_(n\ge0)a_nx^n`

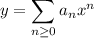
with derivatives

`y'=\displaystyle\sum_(n\ge0)(n+1)a_(n+1)x^n`

`y''=\displaystyle\sum_(n\ge0)(n+2)(n+1)a_(n+2)x^n`

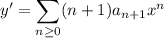
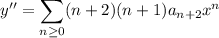
Substituting into the ODE, which appears to be

`(x^2-4)y''+3xy'+y=0,`

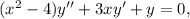
gives

`\displaystyle\sum_(n\ge0)\bigg((n+2)(n+1)a_(n+2)x^(n+2)-4(n+2)(n+1)a_(n+2)x^n+3(n+1)a_(n+1)x^(n+1)+a_nx^n\bigg)=0`

`\displaystyle\sum_(n\ge2)n(n-1)a_nx^n-4\sum_(n\ge0)(n+2)(n+1)a_(n+2)x^n+3\sum_(n\ge1)na_nx^n+\sum_(n\g0)a_nx^n=0`

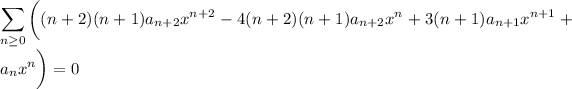
`(a_0-8a_2)+(4a_1-24a_3)x+\displaystyle\sum_(n\ge2)\bigg[(n+1)^2a_n-4(n+2)(n+1)a_(n+2)\bigg]x^n=0`

which gives the recurrence for the coefficients
`a_n`,

`\begin{cases}a_0=a_0\\a_1=a_1\\4(n+2)a_(n+2)=(n+1)a_n&\text{for }n\ge0\end{cases}`

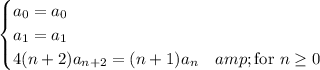
There's dependency between coefficients that are 2 indices apart, so we consider 2 cases.

• If
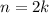  `n=2k`, where
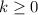  `k\ge0` is an integer, then

`k=0\implies n=0\implies a_0=a_0`

`k=1\implies n=2\implies a_2=\frac1{4\cdot2}a_0=\frac2{4\cdot2^2}a_0=(2!)/(2^4)a_0`

`k=2\implies n=4\implies a_4=\frac3{4\cdot4}a_2=\frac3{4^2\cdot4\cdot2}a_0=(4!)/(2^8(2!)^2)a_0`

`k=3\implies n=6\implies a_6=\frac5{4\cdot6}a_4=(5\cdot3)/(4^3\cdot6\cdot4\cdot2)a_0=(6!)/(2^(12)(3!)^2)a_0`

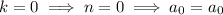
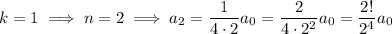
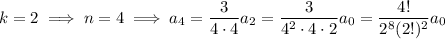
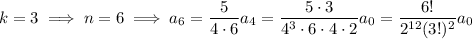
and so on, with the general pattern

`a_(2k)=((2k)!)/(2^(4k)(k!)^2)a_0`

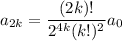
• If
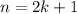  `n=2k+1`, then

`k=0\implies n=1\implies a_1=a_1`

`k=1\implies n=3\implies a_3=\frac2{4\cdot3}a_1=(2^2)/(2^2\cdot3\cdot2)a_1=\frac1{(3!)^2}a_1`

`k=2\implies n=5\implies a_5=\frac4{4\cdot5}a_3=(4\cdot2)/(4^2\cdot5\cdot3)a_1=((2!)^2)/(5!)a_1`

`k=3\implies n=7\implies a_7=\frac6{4\cdot7}a_5=(6\cdot4\cdot2)/(4^3\cdot7\cdot5\cdot3)a_1=((3!)^2)/(7!)a_1`

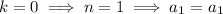
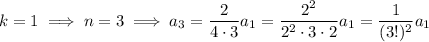
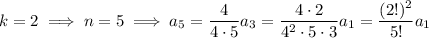
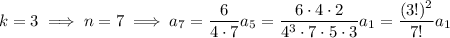
and so on, with

`a_(2k+1)=((k!)^2)/((2k+1)!)a_1`

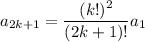
Then the two independent solutions to the ODE are

`\boxed{y_1(x)=\displaystyle a_0\sum_(k\ge0)((2k)!)/(2^(4k)(k!)^2)x^(2k)}`

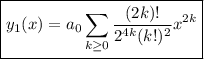
and

`\boxed{y_2(x)=\displaystyle a_1\sum_(k\ge0)((k!)^2)/((2k+1)!)x^(2k+1)}`

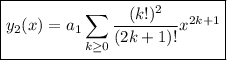
By the ratio test, both series converge for
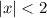`|x|<2`, which also can be deduced from the fact that
`x=\pm2` are singular points for this ODE.