Question

A standardized​ exam's scores are normally distributed. In a recent​ year, the mean test score was 14781478 and the standard deviation was 311311. The test scores of four students selected at random are 18701870​, 12001200​, 21802180​, and 13801380. Find the​ z-scores that correspond to each value and determine whether any of the values are unusual.

Answer 1

Z SCORE FOR 1870 = 1.26

Z SCORE FOR 1200 = -0.89

Z SCORE FOR 2180 = 2.25

Z SCORE FOR 1380 = -0.315

Explanation:

given data:

test score
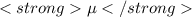`<strong>\mu</strong>` = 1478

standard deviation
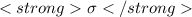`<strong>\sigma</strong>` = 311

z score can be calculated by using below relation

`Z = (X-\mu)/(\sigma)`

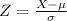
1) Z SCORE FOR 1870

`= (1870-1478)/(311)`

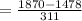
= 1.26

2) Z SCORE FOR 1200

`= (1200-1478)/(311)`

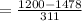
= -0.89

3) Z SCORE FOR 2180

`= (2180-1478)/(311)`

= 2.25

4) Z SCORE FOR 1380

`= (1380-1478)/(311)`

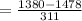
= -0.315

There are no unusual z value.