Answer: 0.0075
Explanation:
Given : The manufacturer of cans of salmon that are supposed to have a net weight of 6 ounces tells you that the net weight is actually a normal random variable with

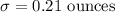
Sample size : n=43
Z-score :

For x= 5.98
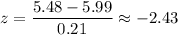
By using standard normal distribution table table , the probability that the mean weight of the sample is less than 5.98 ounces will be :_
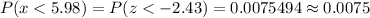
Hence, the probability that the mean weight of the sample is less than 5.98 ounces = 0.0075