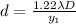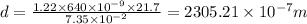Question

Irina finds an unlabeled box of fine needles, and wants to determine how thick they are. A standard ruler will not do the job, as each needle is less than a millimeter thick. So, to find the thickness, she uses a needle to poke a hole in a piece of brown construction paper. Then, she positions a 640 nm laser pointer to shine through the hole and project a circular diffraction pattern on a wall 21.7 m away. She then uses her ruler to measure that the central bright circle is 14.2 cm in diameter. What diameter does Irina calculate for the needle?

Answer 1

`d=(1.22* 640* 10^(-9)* 21.7)/(7.35* 10^(-2))=2305.21* 10^(-7)m`

Step-by-step explanation:

The expression which represent the first diffraction minima by a circular aperture is given by
`d sin\Theta =1.22\lambda`--------eqn 1

The angle through which the first minima is diffracted is given by
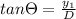`tan\Theta =(y_1)/(D)`---------eqn 2

As
`\Theta` is very small so we can write
`sin\Theta =tan\Theta`

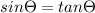
So from eqn 1 and eqn 2 we can write

`y_1=(1.22\lambda D)/(d)`--------eqn 3

Here
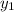`y_1` is the position of first maxima D is the distance of screen from the circular aperture d is the diameter of aperture

It is given that diameter of circular aperture is 14.7 cm so
`y_1=(14.7)/(2)=7.35 \ cm`

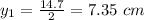
Now putting all these value in eqn 3

`d=(1.22\lambda D)/(y_1)`

`d=(1.22* 640* 10^(-9)* 21.7)/(7.35* 10^(-2))=2305.21* 10^(-7)m`