Question

Lead all chlorate is mixed with hydrolylic acid. Each solution is 0.85 molar. Write balanced, molecular, ionic, and net equations with state labels. Use solubility rules and knowledge of strong acids. Predict how many grams of what solid product can be collected if 125ml lead ll chlorate was treated with with 95 ml of the hydrologic acid. If percent yield was 68 percent how much product was collected and what is the molarity of the chlorate? What is the final concentration of pb2+. Please show work!

Answer 1

Here's what I get

Step-by-step explanation:

Solubility rules

• Salts containing halides are generally soluble. Important exceptions to this rule are halides of silver, mercury, and lead(II).
• All acetates, chlorates, and perchlorates are soluble

So, PbCl₂ is insoluble, and Pb(ClO₃)₂ is soluble.

1. "Molecular" equation

`\rm Pb(ClO_(3))_(2)(aq) + 2HCl(aq) \longrightarrow \, PbCl_(2)(s) + 2HClO_(3)(aq)`

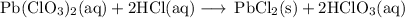
2. Ionic equation

Convert the soluble salts to their hydrated ions.

HCl and HClO₃ are strong acids. Convert them to their ions.

`\rm Pb^(2+)(aq) + 2ClO_(3)^(-)(aq)+ 2H^(+)(aq) + 2Cl^(-)(aq) \longrightarrow \, PbCl_(2)(s) + 2H^(+)(aq) + 2ClO_(3)^(-)(aq)`

3. Net ionic equation

Cancel all ions that appear on both sides of the reaction arrow (in boldface).

`\rm {Pb}^(2+)(aq) + \textbf{2ClO}_(3)^(-)(aq)+ \textbf{2H}^(+)(aq) + 2Cl^(-)(aq) \longrightarrow \, PbCl_(2)(s) + \textbf{2H}^(+)(aq) + \textbf{2ClO}_(3)^(-)(aq)`

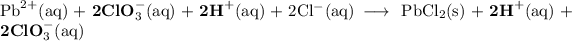
The net ionic equation is

`\rm {Pb}^(2+)(aq) + 2Cl^(-)(aq) \longrightarrow \, PbCl_(2)(s)`

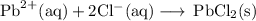
4. Theoretical yield

We have the volumes and concentrations of two reactants, so this is a limiting reactant problem.

We know that we will need a balanced equation with masses, moles, and molar masses of the compounds involved.

(i). Gather all the information in one place with molar masses above the formulas and masses below them.

M_r: 278.11

Pb(ClO₃)₂ + 2HCl ⟶ PbCl₂ + 2HClO₃

Volume/mL: 125 95

c/mol·L⁻¹: 0.85 0.85

(ii) Calculate the moles of each reactant

`\text{Moles of Pb(ClO$_(3)$)}_(2) = \text{0.125 L} * \frac{\text{0.85 mol}}{\text{1 L }} = \text{0.1062 mol}\\\text{Moles of HCl} = \text{0.095 L} * \frac{\text{0.85 mol}}{\text{1 L }} = \text{0.08075 mol}`

(iii) Identify the limiting reactant

Calculate the moles of PbCl₂ we can obtain from each reactant.

From Pb(ClO₃)₂:

The molar ratio of PbCl₂:Pb(ClO₃)₂ is 2:2

Moles of PbCl₂ = 0.1062 × 2/2 =0.1062 mol PbCl₂

From HCl :

The molar ratio of PbCl₂:HCl is 1 mol PbCl₂:2 mol HCl.

Moles of PbCl₂ = 0.08075 × 1/2 = 0.04038 mol PbCl₂

The limiting reactant is HCl because it gives the smaller amount of PbCl₂.

(iv) Calculate the theoretical yield of PbCl₂.

`\text{Theor. yield of PbCl}_(2) = \text{0.0438 mol} * \frac{\text{278.11 g}}{\text{ 1 mol}} = \textbf{11.2 g}`

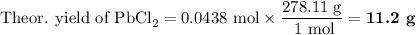
5. Calculate the actual yield of PbCl₂

`\text{Actual yield} = \text{11.2 g theor.} * \frac{\text{ 68 g actual}}{\text{100 g theor,}} = \textbf{7.6 g}`

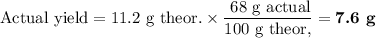
6. Calculate [ClO₃⁻]

Original concentration of Pb(ClO₃)₂ = 0.85 mol·L⁻¹

Original concentration of ClO₃ = 2 × 0.85 = 1.70 mol·L⁻¹

The solution was diluted by the addition of HCl.

Total volume = 125 + 95 =220 mL

c₁V₁ = c₂V₂

1.70 mol·L⁻¹ × 125 mL = c₂ × 220 mL

212.5 mol·L⁻¹ = 200 c₂

c₂ = (212.5 mL)/200 = 1.06 mol·L⁻¹

7. Calculate [Pb²⁺].

Moles of Pb²⁺ originally present = 0.1062 mol

Moles of Pb²⁺removed = 0.04038 mol

Moles of Pb²⁺ remaining = 0.0659 mol

c = 0.0659 mol/0.220 L = 0.299 mol·L⁻¹