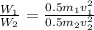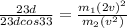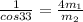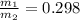Question

Two students are pushing identical crates across a frictionless floor. The crates are initially at rest. Bing applies a horizontal force of 23 N to his crate. Bob, who is shorter than Bing, pushes on his crate at an angle of 33° below the horizontal, also with a force of 23 N. Find the ratio of the masses of the two crates if Bing’s crate is moving at twice the speed of Bob’s crate after they have traveled a distance of 33.5 m across the floor? (20 pts)

Answer 1

`(m_1)/(m_2) = 0.298`

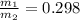
Step-by-step explanation:

As we know that both the crates are moving at different speed after moving 33.5 m

speed of bling crate = 2 (speed of bob crate)

now we know that

Bling apply force horizontal so the acceleration of his crate is given as

`a_1 = (23)/(m_1)`

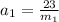
now force of Bob is at 33 degree with the horizontal

so the acceleration of crate of Bob is given as

`a_2 = (23 cos33)/(m_2)`

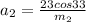
now we know that work done by Bling and bob on their crate is equal to the kinetic energy of the crate

so for Bling's and Bob'scrate we can say

`F. d = (1)/(2)m v^2`

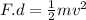
now the ratio of the work done of two is given as

`(W_1)/(W_2) = (0.5 m_1 v_1^2)/(0.5 m_2 v_2^2)`

`(23 d)/(23 d cos33) = (m_1 (2v)^2)/(m_2(v^2))`

`(1)/(cos33) = (4 m_1)/(m_2)`

`(m_1)/(m_2) = 0.298`