Answer:
Acceleration, a = 1.1 m/s²
Step-by-step explanation:
Frequency of source,
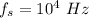
Speed of sound, v = 343 m/s
Frequency of observer,
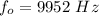
We know that acceleration a of the platform is :
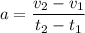 ..............(1)
..............(1)
The frequency detected by the microphone is :
At 1.5 seconds,
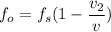

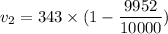
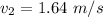
At 3.5 seconds,
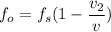


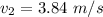
So, equation (1) becomes :
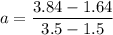
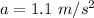
So, the acceleration of the platform is 1.1 m/s². Hence, this is the required solution.