Question

PLEASE HELP ASAP!!!

Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used.
Match each quadratic function with its respective graph.

Answer 1

1: x^2-4x+5

2: -x^2-2x+3

3: x^2-6x+5

Explanation:

Since these are quite simple parabolas, you can just look at the y-intercept of each equation to determine which one matches up.

Answer 2

f(x)=
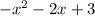`-x^2-2x+3`-Garph II

f(x)=
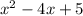`x^2-4x+5`-Graph I

f(x)=
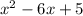`x^2-6x+5`-Graph III

Explanation:

We are given that

f(x)=
`-x^2+2x-3`

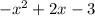
If substitute x=0 then we get f(0)=-3

It means y- intercept =-3

In given graph , there is no y- intercept=-3

It is false.

f(x)=
`-x^2-2x+3`

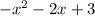
If substitute x=0 the we get

f(0)=3

In second graph y - intercept =3

Substitute x=-1 then we get

f(-1)=-1+2+3=4

Hence, the function match with second graph.

f(x)=
`x^2-4x+5`

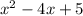
If x=0 then we get

y- intercept =5

If we substitute x=2 then we get

f(1)=4-8+5=1

Hence, function match with First graph.

In third graph

Y- intercept =5

The vertices of parabola is (3,-4)

f(x)=
`x^2-6x+5`

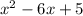
If substitute x=0 then we get

y intercept =5

If we substitute x=3

Then we get

f(3)=
`3^2-6(3)+5`

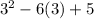
f(3)=9-18+5=-4

Hence, the function match with third graph.