Question

An archer fires an arrow from a bow. The arrow’s mass is 0.088 kg, and an average force of 110 N is exerted by the bowstring over a 0.78 m distance. Calculate the velocity of the arrow just after it is released by the bowstring by two methods: a) Calculate the arrow’s acceleration that is caused by the bowstring, and use the kinematic equations from the first week of class to calculate the velocity at the end of the acceleration. Assume a constant acceleration that corresponds to the given average force.

Answer 1

Step-by-step explanation:

Given that,

Mass of arrow = 0.088 kg

Force = 110 N

Distance = 0.78 m

(a). We need to calculate the acceleration

Using newton's second law

`F= ma`

`a=(F)/(m)`

`a=(110)/(0.088)`

`a=1250\ m/s^2`

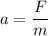
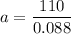
We need to calculate the velocity of the arrow

Using equation of motion

`v^2=u^2+2as`

Where, a = acceleration

s = distance

Put the value in the equation

`v^2=2*1250*0.78`

`v=44.16\ m/s`

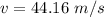
(b). We need to calculate the velocity of the arrow

Using work energy theorem

`W=\Delta K.E`

`F*\Delta x=K.E_(f)-K.E_(i)`

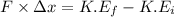
Here, initial kinetic energy is zero

So,

`F*\Delta x=(1)/(2)mv^2`

`v^2=(2F*\Delta x)/(m)`

`v=\sqrt{(2F*\Delta x)/(m)}`

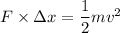
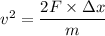
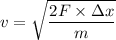
Put the value into the formula

`v=\sqrt{(2*110*0.78)/(0.088)}`

`v=44.16\ m/s`

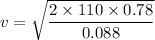
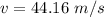
Hence, This is the required solution.