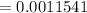Answer with explanation:
Let p be the proportion of adults have heard of the new electronic reader.
Given claim : The accompanying technology display results from a test of the claim that 38% of adults have heard of the new electronic reader.
i.e.

Then , the set of hypothesis will be :-
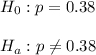
Since, the alternative hypothesis is two tailed , so the test is two-tailed test.
Also, it is given that the sample size :
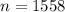
Number of adults showed that they have heard of a new electronic reader=522
So the sample proportion for adults have heard of the new electronic reader :

The test statistic for proportion is given by :-
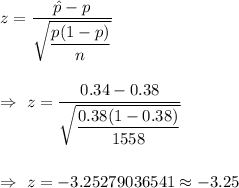
By using standard normal distribution table , the P-value for two tailed test corresponds to the obtained z-value =