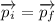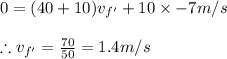Question

A 40 kg girl gets on her 10 kg wagon on level ground. She has two 5 kg bricks with her. She throws the bricks horizontally off the back of the wagon one at a time with a speed of 7 m/s relative to herself. (a) How fast is she moving after throwing the second brick? (b) How fast would she be going if she had thrown both bricks at the same time at a speed of 7 m/s relative to herself?

Answer 1

1) She would be moving at a speed of 1.4 m/s

2) She would be moving at a speed of 1.4 m/s of she throws both the bricks at once.

Step-by-step explanation:

Since the system is isolated we shall conserve the linear momentum of the system to solve the system for required quantities:

We have by conservation of momentum,

`\overrightarrow{p_(i)}=\overrightarrow{p_(f)}`

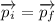
Since initially the system has no momentum thus

After throwing the first brick we have

`\overrightarrow{p_(i)}=\overrightarrow{p_(f)}\\\\(40+10+5)v_(2)+5* (-7m/s)=0\\\\\therefore v_(2)=(35)/(55)=0.63m/s`

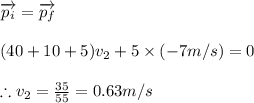
Again conserving the momentum when she throws the second brick we have

`\overrightarrow{p_(i)}=\overrightarrow{p_(f)}`

`(40+10+5)* 0.63m/s=(40+10)v_(f)+5* (-7m/s)\\\\\therefore v_(f)=(55* 0.63+35)/(50)=1.4m/s`

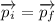
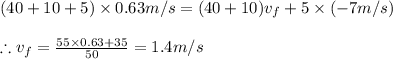
b) If she had thrown both the bricks at the same time analyzing the system in the same manner we have

`\overrightarrow{p_(i)}=\overrightarrow{p_(f)}`

`0=(40+10)v_(f')+10* -7m/s\\\\\therefore v_(f')=(70)/(50)=1.4m/s`