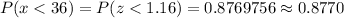Answer: 0.8770
Explanation:
Given : The number of eligible voters aged 18-24 are randomly selected : n=141
The population proportion of eligible voters aged 18-24 : p=0.22
Then, mean :

Standard deviation:
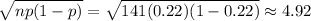
We assume that this is normal distribution.
Let X be a binomial variable.
For x =36
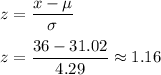
The probability that fewer than 36 voted will be :-