Question

An astronaut is planning a trip to a newly-discovered planet. According to Newton's

law of universal gravitation, the astronaut's weight on the new planet will be greater
than his weight on Earth if:
The new planet has less mass than Earth but the same radius.
The new planet has montimass than Earth but the same radius.
The size of the planet doesn't matter. Weight is the same everywhere in
universe.
The new planet has less mass than Earth and a larger radius.

Answer 1

"The new planet has more mass than Earth but the same radius"

Step-by-step explanation:

Newton's universal gravitational equation is:

`F=G(m*M)/(r^2)`

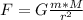
Where G is the gravitational constant

m is the astronaut's mass

M is the mass of the planet

r is the radius of the planet

F is the gravitational force

The magnitude of gravitational acceleration is:

`g=G(M)/(r^2)`

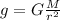
The astronaut's weight depends on the gravitational acceleration of the planet and its mass. Since the mass is the same in any part of space then we consider gravitational acceleration

Gravitational acceleration increases when the planet's mass increases or when its radius decreases.

Gravitational acceleration decreases when the planet's mass is small or when its radius increases

Therefore the answer is the second option: "The new planet has more mass than Earth but the same radius"