Question

Based on FAA estimates the average age of the fleets of the 10 largest U.S. commercial passenger carriers is 13.4 years with a standard deviation of 1.7 years. Suppose that 40 airplanes were randomly selected from the fleets of these 10 carriers and were inspected for cracks in these airplanes that are considered too large for flying. What is the probability that the average age of these 40 airplanes is at least 14 years old

Answer 1

Answer : 0.0129

Explanation:

Given : Based on FAA estimates the average age of the fleets of the 10 largest U.S. commercial passenger carriers is
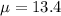`\mu=13.4` years and standard deviation is
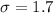`\sigma=1.7` years.

Sample size :
`n=40`

Let X be the random variable that represents the age of fleets.

We assume that the ages of the fleets of the 10 largest U.S. commercial passenger carriers are normally distributed.

For z-score,

`z=(x-\mu)/((\sigma)/(√(n)))`

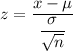
For x=14

`z=(14-13.4)/((1.7)/(√(40)))\approx2.23`

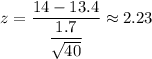
By using the standard normal distribution table , the probability that the average age of these 40 airplanes is at least 14 years old will be :-

`P(x\geq 14)=P(z\geq2.23)\\\\=1-P(z<2.23)\\\\1- 0.9871262=0.0128738\approx0.0129`

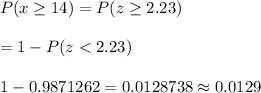
Hence, the required probability = 0.0129